Moving Window Statistics¶
This chapter describes routines for computing moving window statistics (also called rolling statistics and running statistics), using a window around a sample which is used to calculate various local statistical properties of an input data stream. The window is then slid forward by one sample to process the next data point and so on.
The functions described in this chapter are declared in the header file
gsl_movstat.h.
Introduction¶
This chapter is concerned with calculating various statistics from
subsets of a given dataset. The main idea is to compute statistics
in the vicinity of a given data sample by defining a window which
includes the sample itself as well as some specified number of samples
before and after the sample in question. For a sample 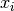 , we
define a window
, we
define a window 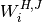 as
as
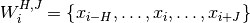
The parameters 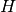 and
and 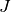 are non-negative integers specifying
the number of samples to include before and after the sample
are non-negative integers specifying
the number of samples to include before and after the sample 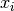 .
Statistics such as the mean and standard deviation of the window
.
Statistics such as the mean and standard deviation of the window 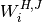 may be computed, and then the window is shifted forward by one sample to
focus on
may be computed, and then the window is shifted forward by one sample to
focus on 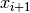 . The total number of samples in the window is
. The total number of samples in the window is
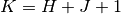 . To define a symmetric window centered on
. To define a symmetric window centered on 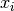 ,
one would set
,
one would set 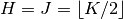 .
.
Handling Endpoints¶
When processing samples near the ends of the input signal, there will not
be enough samples to fill the window 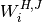 defined above.
Therefore the user must specify how to construct the windows near the end points.
This is done by passing an input argument of type
defined above.
Therefore the user must specify how to construct the windows near the end points.
This is done by passing an input argument of type gsl_movstat_end_t:
-
type gsl_movstat_end_t¶
This data type specifies how to construct windows near end points and can be selected from the following choices:
-
GSL_MOVSTAT_END_PADZERO¶
With this option, a full window of length
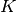 will be constructed
by inserting zeros into the window near the signal end points. Effectively,
the input signal is modified to
will be constructed
by inserting zeros into the window near the signal end points. Effectively,
the input signal is modified to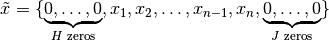
to ensure a well-defined window for all
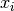 .
.
-
GSL_MOVSTAT_END_PADVALUE¶
With this option, a full window of length
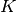 will be constructed
by padding the window with the first and last sample in the input signal.
Effectively, the input signal is modified to
will be constructed
by padding the window with the first and last sample in the input signal.
Effectively, the input signal is modified to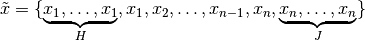
-
GSL_MOVSTAT_END_TRUNCATE¶
With this option, no padding is performed, and the windows are simply truncated as the end points are approached.
-
GSL_MOVSTAT_END_PADZERO¶
Allocation for Moving Window Statistics¶
-
type gsl_movstat_workspace¶
The moving window statistical routines use a common workspace.
-
gsl_movstat_workspace *gsl_movstat_alloc(const size_t K)¶
This function allocates a workspace for computing symmetric, centered moving statistics with a window length of
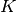 samples. In this case,
samples. In this case, 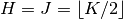 . The size of the workspace
is
. The size of the workspace
is 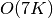 .
.
-
gsl_movstat_workspace *gsl_movstat_alloc2(const size_t H, const size_t J)¶
This function allocates a workspace for computing moving statistics using a window with
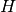 samples prior to the current sample, and
samples prior to the current sample, and 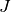 samples after the current sample. The
total window size is
samples after the current sample. The
total window size is 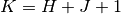 . The size of the workspace is
. The size of the workspace is 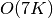 .
.
-
void *gsl_movstat_free(gsl_movstat_workspace *w)¶
This function frees the memory associated with
w.
Moving Mean¶
The moving window mean calculates the mean of the values of each window 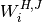 .
.
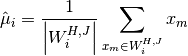
Here, 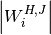 represents the number of elements in the window
represents the number of elements in the window
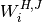 . This will normally be
. This will normally be 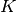 , unless the
, unless the GSL_MOVSTAT_END_TRUNCATE
option is selected, in which case it could be less than 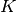 near the signal end points.
near the signal end points.
-
int gsl_movstat_mean(const gsl_movstat_end_t endtype, const gsl_vector *x, gsl_vector *y, gsl_movstat_workspace *w)¶
This function computes the moving window mean of the input vector
x, storing the output iny. The parameterendtypespecifies how windows near the ends of the input should be handled. It is allowed to havex=yfor an in-place moving mean.
Moving Variance and Standard Deviation¶
The moving window variance calculates the sample variance of the values of each window 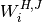 ,
defined by
,
defined by
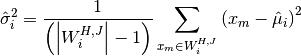
where 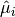 is the mean of
is the mean of 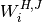 defined above. The standard deviation
defined above. The standard deviation 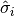 is the square root of the variance.
is the square root of the variance.
-
int gsl_movstat_variance(const gsl_movstat_end_t endtype, const gsl_vector *x, gsl_vector *y, gsl_movstat_workspace *w)¶
This function computes the moving window variance of the input vector
x, storing the output iny. The parameterendtypespecifies how windows near the ends of the input should be handled. It is allowed to havex=yfor an in-place moving variance.
-
int gsl_movstat_sd(const gsl_movstat_end_t endtype, const gsl_vector *x, gsl_vector *y, gsl_movstat_workspace *w)¶
This function computes the moving window standard deviation of the input vector
x, storing the output iny. The parameterendtypespecifies how windows near the ends of the input should be handled. It is allowed to havex=yfor an in-place moving standard deviation.
Moving Minimum and Maximum¶
The moving minimum/maximum calculates the minimum and maximum values of
each window 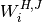 .
.
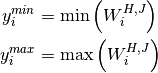
-
int gsl_movstat_min(const gsl_movstat_end_t endtype, const gsl_vector *x, gsl_vector *y, gsl_movstat_workspace *w)¶
This function computes the moving minimum of the input vector
x, storing the result iny. The parameterendtypespecifies how windows near the ends of the input should be handled. It is allowed to havex=yfor an in-place moving minimum.
-
int gsl_movstat_max(const gsl_movstat_end_t endtype, const gsl_vector *x, gsl_vector *y, gsl_movstat_workspace *w)¶
This function computes the moving maximum of the input vector
x, storing the result iny. The parameterendtypespecifies how windows near the ends of the input should be handled. It is allowed to havex=yfor an in-place moving maximum.
-
int gsl_movstat_minmax(const gsl_movstat_end_t endtype, const gsl_vector *x, gsl_vector *y_min, gsl_vector *y_max, gsl_movstat_workspace *w)¶
This function computes the moving minimum and maximum of the input vector
x, storing the window minimums iny_minand the window maximums iny_max. The parameterendtypespecifies how windows near the ends of the input should be handled.
Moving Sum¶
The moving window sum calculates the sum of the values of each window 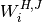 .
.
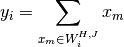
-
int gsl_movstat_sum(const gsl_movstat_end_t endtype, const gsl_vector *x, gsl_vector *y, gsl_movstat_workspace *w)¶
This function computes the moving window sum of the input vector
x, storing the output iny. The parameterendtypespecifies how windows near the ends of the input should be handled. It is allowed to havex=yfor an in-place moving sum.
Moving Median¶
The moving median calculates the median of the window 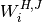 for
each sample
for
each sample 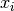 :
:
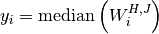
-
int gsl_movstat_median(const gsl_movstat_end_t endtype, const gsl_vector *x, gsl_vector *y, gsl_movstat_workspace *w)¶
This function computes the moving median of the input vector
x, storing the output iny. The parameterendtypespecifies how windows near the ends of the input should be handled. It is allowed forx=yfor an in-place moving window median.
Robust Scale Estimation¶
A common problem in statistics is to quantify the dispersion (also known as the variability, scatter, and spread) of a set of data. Often this is done by calculating the variance or standard deviation. However these statistics are strongly influenced by outliers, and can often provide erroneous results when even a small number of outliers are present.
Several useful statistics have emerged to provide robust estimates of scale which are not as susceptible to data outliers. A few of these statistical scale estimators are described below.
Moving MAD¶
The median absolute deviation (MAD) for the window 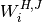 is defined
to be the median of the absolute deviations from the window’s median:
is defined
to be the median of the absolute deviations from the window’s median:
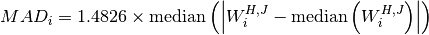
The factor of 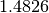 makes the MAD an unbiased estimator of the standard deviation
for Gaussian data. The MAD has an efficiency of 37%. See here for more information.
makes the MAD an unbiased estimator of the standard deviation
for Gaussian data. The MAD has an efficiency of 37%. See here for more information.
-
int gsl_movstat_mad0(const gsl_movstat_end_t endtype, const gsl_vector *x, gsl_vector *xmedian, gsl_vector *xmad, gsl_movstat_workspace *w)¶
-
int gsl_movstat_mad(const gsl_movstat_end_t endtype, const gsl_vector *x, gsl_vector *xmedian, gsl_vector *xmad, gsl_movstat_workspace *w)¶
These functions compute the moving MAD of the input vector
xand store the result inxmad. The medians of each window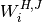 are stored in
are stored in xmedianon output. The inputsx,xmedian, andxmadmust all be the same length. The parameterendtypespecifies how windows near the ends of the input should be handled. The functionmad0does not include the scale factor of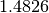 , while the
function
, while the
function maddoes include this factor.
Moving QQR¶
The q-quantile range (QQR) is the difference between the 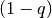 and
and 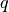 quantiles
of a set of data,
quantiles
of a set of data,
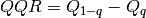
The case 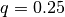 corresponds to the well-known interquartile range (IQR), which
is the difference between the 75th and 25th percentiles of a set of data. The QQR is
a trimmed estimator, the main idea being to discard the largest and smallest values in
a data window and compute a scale estimate from the remaining middle values. In the case
of the IQR, the largest and smallest 25% of the data are discarded and the scale is
estimated from the remaining (middle) 50%.
corresponds to the well-known interquartile range (IQR), which
is the difference between the 75th and 25th percentiles of a set of data. The QQR is
a trimmed estimator, the main idea being to discard the largest and smallest values in
a data window and compute a scale estimate from the remaining middle values. In the case
of the IQR, the largest and smallest 25% of the data are discarded and the scale is
estimated from the remaining (middle) 50%.
-
int gsl_movstat_qqr(const gsl_movstat_end_t endtype, const gsl_vector *x, const double q, gsl_vector *xqqr, gsl_movstat_workspace *w)¶
This function computes the moving QQR of the input vector
xand stores the q-quantile ranges of each window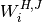 in
in xqqr. The quantile parameterqmust be between and
and 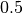 . The input
. The input 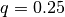 corresponds to the IQR.
The inputs
corresponds to the IQR.
The inputs xandxqqrmust be the same length. The parameterendtypespecifies how windows near the ends of the input should be handled.
Moving 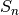 ¶
¶
The 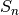 statistic proposed by Croux and Rousseeuw is based on pairwise differences between
all samples in the window. It has an efficiency of 58%, significantly higher than the MAD.
See here for more information.
statistic proposed by Croux and Rousseeuw is based on pairwise differences between
all samples in the window. It has an efficiency of 58%, significantly higher than the MAD.
See here for more information.
-
int gsl_movstat_Sn(const gsl_movstat_end_t endtype, const gsl_vector *x, gsl_vector *xscale, gsl_movstat_workspace *w)¶
This function computes the moving
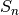 of the input vector
of the input vector xand stores the output inxscale. The inputsxandxscalemust be the same length. The parameterendtypespecifies how windows near the ends of the input should be handled. It is allowed forx=xscalefor an in-place moving window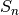 .
.
Moving 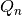 ¶
¶
The 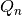 statistic proposed by Croux and Rousseeuw is loosely based on the Hodges-Lehmann location
estimator. It has a relatively high efficiency of 82%. See here for more information.
statistic proposed by Croux and Rousseeuw is loosely based on the Hodges-Lehmann location
estimator. It has a relatively high efficiency of 82%. See here for more information.
-
int gsl_movstat_Qn(const gsl_movstat_end_t endtype, const gsl_vector *x, gsl_vector *xscale, gsl_movstat_workspace *w)¶
This function computes the moving
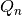 of the input vector
of the input vector xand stores the output inxscale. The inputsxandxscalemust be the same length. The parameterendtypespecifies how windows near the ends of the input should be handled. It is allowed forx=xscalefor an in-place moving window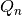 .
.
User-defined Moving Statistics¶
GSL offers an interface for users to define their own moving window statistics
functions, without needing to implement the edge-handling and accumulator
machinery. This can be done by explicitly constructing the windows
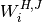 for a given input signal (
for a given input signal (gsl_movstat_fill()), or by calculating a user-defined
function for each window automatically. In order to apply a user-defined
function to each window, users must define a variable of type
gsl_movstat_function to pass into gsl_movstat_apply().
This structure is defined as follows.
-
type gsl_movstat_function¶
Structure specifying user-defined moving window statistical function:
typedef struct { double (* function) (const size_t n, double x[], void * params); void * params; } gsl_movstat_function;
This structure contains a pointer to the user-defined function as well as possible parameters to pass to the function.
-
double (*function)(const size_t n, double x[], void *params)¶
This function returns the user-defined statistic of the array
xof lengthn. User-specified parameters are passed in viaparams. It is allowed to modify the arrayx.
-
void *params¶
User-specified parameters to be passed into the function.
-
double (*function)(const size_t n, double x[], void *params)¶
-
int gsl_movstat_apply(const gsl_movstat_end_t endtype, const gsl_movstat_function *F, const gsl_vector *x, gsl_vector *y, gsl_movstat_workspace *w)¶
This function applies the user-defined moving window statistic specified in
Fto the input vectorx, storing the output iny. The parameterendtypespecifies how windows near the ends of the input should be handled. It is allowed forx=yfor an in-place moving window calculation.
-
size_t gsl_movstat_fill(const gsl_movstat_end_t endtype, const gsl_vector *x, const size_t idx, const size_t H, const size_t J, double *window)¶
This function explicitly constructs the sliding window for the input vector
xwhich is centered on the sampleidx. On output, the arraywindowwill contain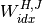 . The number of samples to the left and right
of the sample
. The number of samples to the left and right
of the sample idxare specified byHandJrespectively. The parameterendtypespecifies how windows near the ends of the input should be handled. The function returns the size of the window.
Accumulators¶
Many of the algorithms of this chapter are based on an accumulator design, which process the input vector one sample at a time, updating calculations of the desired statistic for the current window. Each accumulator is stored in the following structure:
-
type gsl_movstat_accum¶
Structure specifying accumulator for moving window statistics:
typedef struct { size_t (* size) (const size_t n); int (* init) (const size_t n, void * vstate); int (* insert) (const double x, void * vstate); int (* delete) (void * vstate); int (* get) (void * params, double * result, const void * vstate); } gsl_movstat_accum;
The structure contains function pointers responsible for performing different tasks for the accumulator.
-
size_t (*size)(const size_t n)¶
This function returns the size of the workspace (in bytes) needed by the accumulator for a moving window of length
n.
-
int (*init)(const size_t n, void *vstate)¶
This function initializes the workspace
vstatefor a moving window of lengthn.
-
int (*insert)(const double x, void *vstate)¶
This function inserts a single sample
xinto the accumulator, updating internal calculations of the desired statistic. If the accumulator is full (i.e.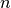 samples
have already been inserted), then the oldest sample is deleted from the accumulator.
samples
have already been inserted), then the oldest sample is deleted from the accumulator.
-
int (*delete)(void *vstate)¶
This function deletes the oldest sample from the accumulator, updating internal calculations of the desired statistic.
-
int (*get)(void *params, double *result, const void *vstate)¶
This function stores the desired statistic for the current window in
result. The inputparamsspecifies optional parameters for calculating the statistic.
-
size_t (*size)(const size_t n)¶
The following accumulators of type gsl_movstat_accum are defined by GSL to perform moving window statistics
calculations.
-
gsl_movstat_accum *gsl_movstat_accum_min¶
-
gsl_movstat_accum *gsl_movstat_accum_max¶
-
gsl_movstat_accum *gsl_movstat_accum_minmax¶
These accumulators calculate moving window minimum/maximums efficiently, using the algorithm of D. Lemire.
-
gsl_movstat_accum *gsl_movstat_accum_mean¶
-
gsl_movstat_accum *gsl_movstat_accum_sd¶
-
gsl_movstat_accum *gsl_movstat_accum_variance¶
These accumulators calculate the moving window mean, standard deviation, and variance, using the algorithm of B. P. Welford.
-
gsl_movstat_accum *gsl_movstat_accum_median¶
This accumulator calculates the moving window median using the min/max heap algorithm of Härdle and Steiger.
-
gsl_movstat_accum *gsl_movstat_accum_Sn¶
-
gsl_movstat_accum *gsl_movstat_accum_Qn¶
These accumulators calculate the moving window
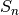 and
and 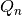 statistics
developed by Croux and Rousseeuw.
statistics
developed by Croux and Rousseeuw.
-
gsl_movstat_accum *gsl_movstat_accum_sum¶
This accumulator calculates the moving window sum.
-
gsl_movstat_accum *gsl_movstat_accum_qqr¶
This accumulator calculates the moving window q-quantile range.
Examples¶
Example 1¶
The following example program computes the moving mean, minimum and maximum of a noisy
sinusoid signal of length 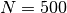 with a symmetric moving window of size
with a symmetric moving window of size 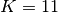 .
.
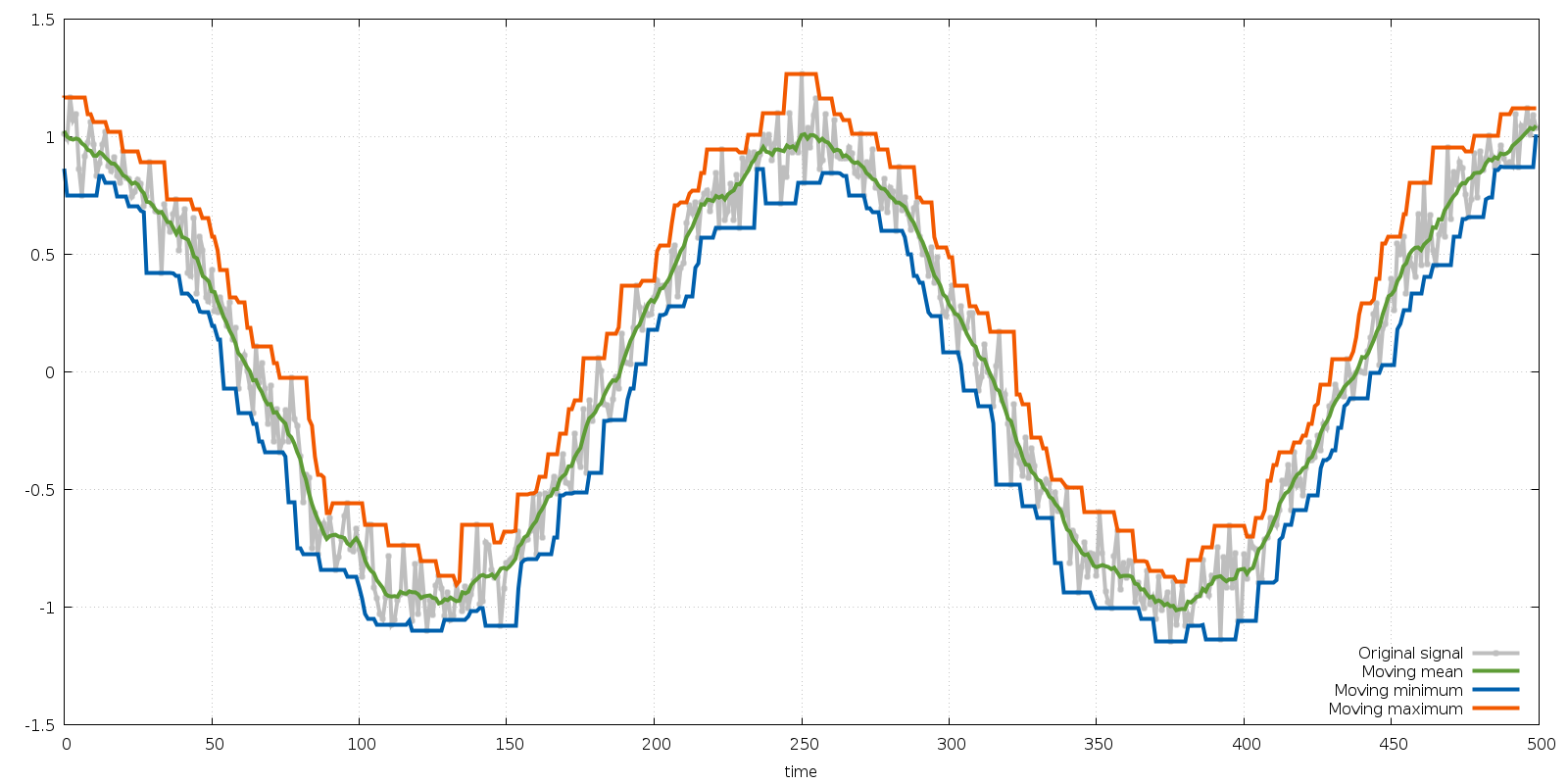
Fig. 6 Original signal time series (gray) with moving mean (green), moving minimum (blue), and moving maximum (orange).¶
The program is given below.
#include <stdio.h>
#include <stdlib.h>
#include <gsl/gsl_math.h>
#include <gsl/gsl_movstat.h>
#include <gsl/gsl_rng.h>
#include <gsl/gsl_randist.h>
#include <gsl/gsl_vector.h>
int
main(void)
{
const size_t N = 500; /* length of time series */
const size_t K = 11; /* window size */
gsl_movstat_workspace * w = gsl_movstat_alloc(K);
gsl_vector *x = gsl_vector_alloc(N);
gsl_vector *xmean = gsl_vector_alloc(N);
gsl_vector *xmin = gsl_vector_alloc(N);
gsl_vector *xmax = gsl_vector_alloc(N);
gsl_rng *r = gsl_rng_alloc(gsl_rng_default);
size_t i;
for (i = 0; i < N; ++i)
{
double xi = cos(4.0 * M_PI * i / (double) N);
double ei = gsl_ran_gaussian(r, 0.1);
gsl_vector_set(x, i, xi + ei);
}
/* compute moving statistics */
gsl_movstat_mean(GSL_MOVSTAT_END_PADVALUE, x, xmean, w);
gsl_movstat_minmax(GSL_MOVSTAT_END_PADVALUE, x, xmin, xmax, w);
/* print results */
for (i = 0; i < N; ++i)
{
printf("%zu %f %f %f %f\n",
i,
gsl_vector_get(x, i),
gsl_vector_get(xmean, i),
gsl_vector_get(xmin, i),
gsl_vector_get(xmax, i));
}
gsl_vector_free(x);
gsl_vector_free(xmean);
gsl_rng_free(r);
gsl_movstat_free(w);
return 0;
}
Example 2: Robust Scale¶
The following example program analyzes a time series of length 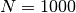 composed
of Gaussian random variates with zero mean whose standard deviation changes in a piecewise constant fashion
as shown in the table below.
composed
of Gaussian random variates with zero mean whose standard deviation changes in a piecewise constant fashion
as shown in the table below.
Sample Range |
|
|---|---|
1-200 |
1.0 |
201-450 |
5.0 |
451-600 |
1.0 |
601-850 |
3.0 |
851-1000 |
5.0 |
Additionally, about 1% of the samples are perturbed to represent outliers by adding
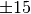 to the random Gaussian variate.
The program calculates the moving statistics MAD, IQR,
to the random Gaussian variate.
The program calculates the moving statistics MAD, IQR, 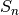 ,
, 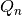 , and
the standard deviation using a symmetric moving window of length
, and
the standard deviation using a symmetric moving window of length 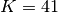 . The results are shown in
Fig. 7.
. The results are shown in
Fig. 7.
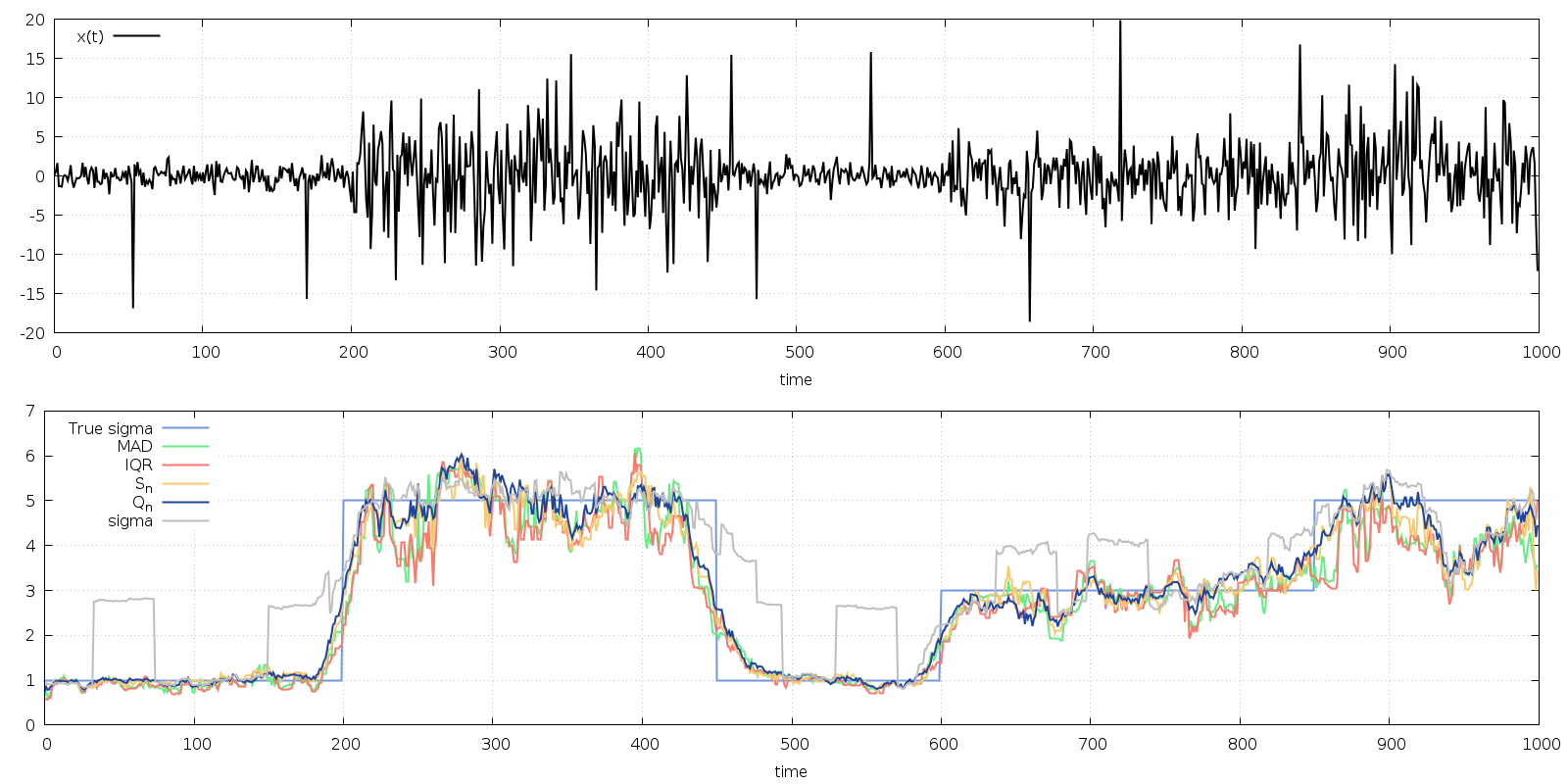
Fig. 7 Top: time series of piecewise constant variance. Bottom: scale estimates using a moving
window; the true sigma value is in light blue, MAD in green, IQR in red, 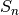 in yellow, and
in yellow, and
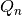 in dark blue. The moving standard deviation is shown in gray.¶
in dark blue. The moving standard deviation is shown in gray.¶
The robust statistics follow the true standard deviation piecewise changes well, without being influenced by the outliers. The moving standard deviation (gray curve) is heavily influenced by the presence of the outliers. The program is given below.
#include <stdio.h>
#include <stdlib.h>
#include <gsl/gsl_math.h>
#include <gsl/gsl_movstat.h>
#include <gsl/gsl_rng.h>
#include <gsl/gsl_randist.h>
#include <gsl/gsl_vector.h>
int
main(void)
{
const size_t N = 1000; /* length of time series */
const double sigma[] = { 1.0, 5.0, 1.0, 3.0, 5.0 }; /* variances */
const size_t N_sigma[] = { 200, 450, 600, 850, 1000 }; /* samples where variance changes */
const size_t K = 41; /* window size */
gsl_vector *x = gsl_vector_alloc(N);
gsl_vector *xmedian = gsl_vector_alloc(N);
gsl_vector *xmad = gsl_vector_alloc(N);
gsl_vector *xiqr = gsl_vector_alloc(N);
gsl_vector *xSn = gsl_vector_alloc(N);
gsl_vector *xQn = gsl_vector_alloc(N);
gsl_vector *xsd = gsl_vector_alloc(N);
gsl_rng *r = gsl_rng_alloc(gsl_rng_default);
gsl_movstat_workspace * w = gsl_movstat_alloc(K);
size_t idx = 0;
size_t i;
for (i = 0; i < N; ++i)
{
double gi = gsl_ran_gaussian(r, sigma[idx]);
double u = gsl_rng_uniform(r);
double outlier = (u < 0.01) ? 15.0*GSL_SIGN(gi) : 0.0;
double xi = gi + outlier;
gsl_vector_set(x, i, xi);
if (i == N_sigma[idx] - 1)
++idx;
}
/* compute moving statistics */
gsl_movstat_mad(GSL_MOVSTAT_END_TRUNCATE, x, xmedian, xmad, w);
gsl_movstat_qqr(GSL_MOVSTAT_END_TRUNCATE, x, 0.25, xiqr, w);
gsl_movstat_Sn(GSL_MOVSTAT_END_TRUNCATE, x, xSn, w);
gsl_movstat_Qn(GSL_MOVSTAT_END_TRUNCATE, x, xQn, w);
gsl_movstat_sd(GSL_MOVSTAT_END_TRUNCATE, x, xsd, w);
/* scale IQR by factor to approximate standard deviation */
gsl_vector_scale(xiqr, 0.7413);
/* print results */
idx = 0;
for (i = 0; i < N; ++i)
{
printf("%zu %f %f %f %f %f %f %f\n",
i,
gsl_vector_get(x, i),
sigma[idx],
gsl_vector_get(xmad, i),
gsl_vector_get(xiqr, i),
gsl_vector_get(xSn, i),
gsl_vector_get(xQn, i),
gsl_vector_get(xsd, i));
if (i == N_sigma[idx] - 1)
++idx;
}
gsl_vector_free(x);
gsl_vector_free(xmedian);
gsl_vector_free(xmad);
gsl_vector_free(xiqr);
gsl_vector_free(xSn);
gsl_vector_free(xQn);
gsl_vector_free(xsd);
gsl_rng_free(r);
gsl_movstat_free(w);
return 0;
}
Example 3: User-defined Moving Window¶
This example program illustrates how a user can define their own moving window function to apply
to an input vector. It constructs a random noisy time series of length 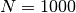 with
some outliers added. Then it applies a moving window trimmed mean to the time series with
trim parameter
with
some outliers added. Then it applies a moving window trimmed mean to the time series with
trim parameter 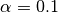 . The length of the moving window is
. The length of the moving window is 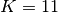 , so
the smallest and largest sample of each window is discarded prior to computing the mean.
The results are shown in Fig. 8.
, so
the smallest and largest sample of each window is discarded prior to computing the mean.
The results are shown in Fig. 8.
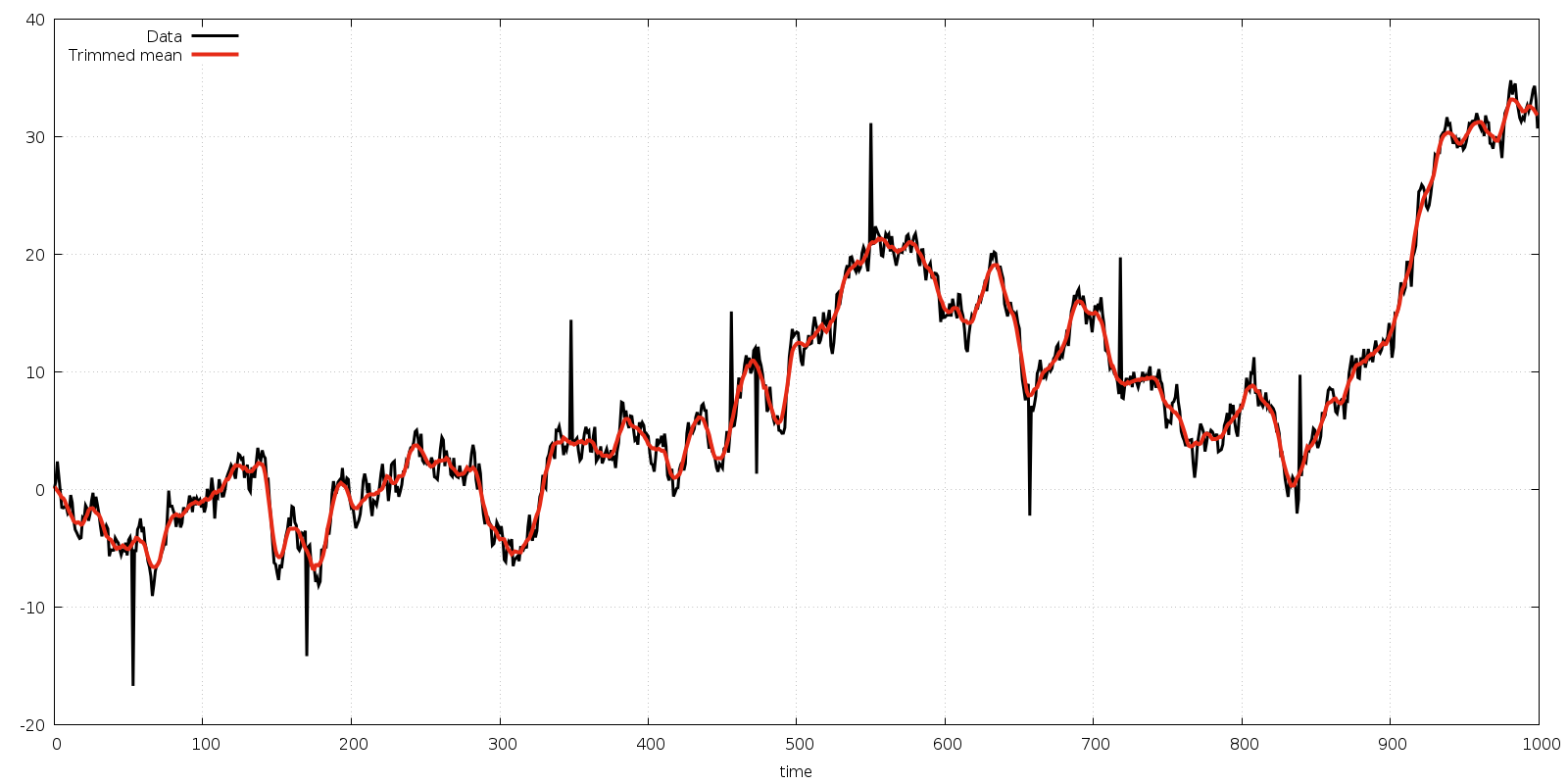
Fig. 8 Noisy time series data (black) with moving window trimmed mean (red)¶
The program is given below.
#include <stdio.h>
#include <stdlib.h>
#include <gsl/gsl_math.h>
#include <gsl/gsl_movstat.h>
#include <gsl/gsl_rng.h>
#include <gsl/gsl_randist.h>
#include <gsl/gsl_vector.h>
#include <gsl/gsl_sort.h>
#include <gsl/gsl_statistics.h>
double
func(const size_t n, double x[], void * params)
{
const double alpha = *(double *) params;
gsl_sort(x, 1, n);
return gsl_stats_trmean_from_sorted_data(alpha, x, 1, n);
}
int
main(void)
{
const size_t N = 1000; /* length of time series */
const size_t K = 11; /* window size */
double alpha = 0.1; /* trimmed mean parameter */
gsl_vector *x = gsl_vector_alloc(N); /* input vector */
gsl_vector *y = gsl_vector_alloc(N); /* filtered output vector for alpha1 */
gsl_rng *r = gsl_rng_alloc(gsl_rng_default);
gsl_movstat_workspace *w = gsl_movstat_alloc(K);
gsl_movstat_function F;
size_t i;
double sum = 0.0;
/* generate input signal */
for (i = 0; i < N; ++i)
{
double ui = gsl_ran_gaussian(r, 1.0);
double outlier = (gsl_rng_uniform(r) < 0.01) ? 10.0*GSL_SIGN(ui) : 0.0;
sum += ui;
gsl_vector_set(x, i, sum + outlier);
}
/* apply moving window function */
F.function = func;
F.params = α
gsl_movstat_apply(GSL_MOVSTAT_END_PADVALUE, &F, x, y, w);
/* print results */
for (i = 0; i < N; ++i)
{
double xi = gsl_vector_get(x, i);
double yi = gsl_vector_get(y, i);
printf("%f %f\n", xi, yi);
}
gsl_vector_free(x);
gsl_vector_free(y);
gsl_rng_free(r);
gsl_movstat_free(w);
return 0;
}
References and Further Reading¶
The following publications are relevant to the algorithms described in this chapter,
W.Hardle and W. Steiger, Optimal Median Smoothing, Appl. Statist., 44 (2), 1995.
D. Lemire, Streaming Maximum-Minimum Filter Using No More than Three Comparisons per Element, Nordic Journal of Computing, 13 (4), 2006 (https://arxiv.org/abs/cs/0610046).
B. P. Welford, Note on a method for calculating corrected sums of squares and products, Technometrics, 4 (3), 1962.