Running Statistics¶
This chapter describes routines for computing running statistics, also known as online statistics, of data. These routines are suitable for handling large datasets for which it may be inconvenient or impractical to store in memory all at once. The data can be processed in a single pass, one point at a time. Each time a data point is added to the accumulator, internal parameters are updated in order to compute the current mean, variance, standard deviation, skewness, and kurtosis. These statistics are exact, and are updated with numerically stable single-pass algorithms. The median and arbitrary quantiles are also available, however these calculations use algorithms which provide approximations, and grow more accurate as more data is added to the accumulator.
The functions described in this chapter are declared in the header file
gsl_rstat.h.
Initializing the Accumulator¶
-
type gsl_rstat_workspace¶
This workspace contains parameters used to calculate various statistics and are updated after each data point is added to the accumulator.
-
gsl_rstat_workspace *gsl_rstat_alloc(void)¶
This function allocates a workspace for computing running statistics. The size of the workspace is
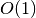 .
.
-
void gsl_rstat_free(gsl_rstat_workspace *w)¶
This function frees the memory associated with the workspace
w.
-
int gsl_rstat_reset(gsl_rstat_workspace *w)¶
This function resets the workspace
wto its initial state, so it can begin working on a new set of data.
Adding Data to the Accumulator¶
-
int gsl_rstat_add(const double x, gsl_rstat_workspace *w)¶
This function adds the data point
xto the statistical accumulator, updating calculations of the mean, variance, standard deviation, skewness, kurtosis, and median.
-
size_t gsl_rstat_n(const gsl_rstat_workspace *w)¶
This function returns the number of data so far added to the accumulator.
Current Statistics¶
-
double gsl_rstat_min(const gsl_rstat_workspace *w)¶
This function returns the minimum value added to the accumulator.
-
double gsl_rstat_max(const gsl_rstat_workspace *w)¶
This function returns the maximum value added to the accumulator.
-
double gsl_rstat_mean(const gsl_rstat_workspace *w)¶
This function returns the mean of all data added to the accumulator, defined as
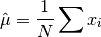
-
double gsl_rstat_variance(const gsl_rstat_workspace *w)¶
This function returns the variance of all data added to the accumulator, defined as
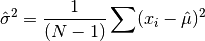
-
double gsl_rstat_sd(const gsl_rstat_workspace *w)¶
This function returns the standard deviation of all data added to the accumulator, defined as the square root of the variance given above.
-
double gsl_rstat_sd_mean(const gsl_rstat_workspace *w)¶
This function returns the standard deviation of the mean, defined as
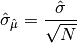
-
double gsl_rstat_rms(const gsl_rstat_workspace *w)¶
This function returns the root mean square of all data added to the accumulator, defined as
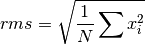
-
double gsl_rstat_skew(const gsl_rstat_workspace *w)¶
This function returns the skewness of all data added to the accumulator, defined as
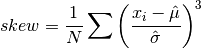
-
double gsl_rstat_kurtosis(const gsl_rstat_workspace *w)¶
This function returns the kurtosis of all data added to the accumulator, defined as
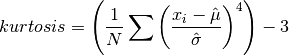
-
double gsl_rstat_median(gsl_rstat_workspace *w)¶
This function returns an estimate of the median of the data added to the accumulator.
-
double gsl_rstat_norm(const gsl_rstat_workspace *w)¶
This function returns the Euclidean norm of all data added to the accumulator, defined as
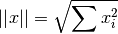
Quantiles¶
The functions in this section estimate quantiles dynamically without
storing the entire dataset, using the algorithm of Jain and Chlamtec, 1985.
Only five points (markers) are stored which represent the minimum
and maximum of the data, as well as current estimates of the
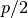 -,
-, 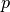 -, and
-, and 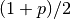 -quantiles. Each time
a new data point is added, the marker positions and heights are
updated.
-quantiles. Each time
a new data point is added, the marker positions and heights are
updated.
-
type gsl_rstat_quantile_workspace¶
This workspace contains parameters for estimating quantiles of the current dataset
-
gsl_rstat_quantile_workspace *gsl_rstat_quantile_alloc(const double p)¶
This function allocates a workspace for the dynamic estimation of
p-quantiles, wherepis between and
and 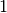 .
The median corresponds to
.
The median corresponds to 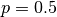 . The size of the workspace
is
. The size of the workspace
is 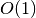 .
.
-
void gsl_rstat_quantile_free(gsl_rstat_quantile_workspace *w)¶
This function frees the memory associated with the workspace
w.
-
int gsl_rstat_quantile_reset(gsl_rstat_quantile_workspace *w)¶
This function resets the workspace
wto its initial state, so it can begin working on a new set of data.
-
int gsl_rstat_quantile_add(const double x, gsl_rstat_quantile_workspace *w)¶
This function updates the estimate of the
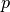 -quantile with
the new data point
-quantile with
the new data point x.
-
double gsl_rstat_quantile_get(gsl_rstat_quantile_workspace *w)¶
This function returns the current estimate of the
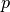 -quantile.
-quantile.
Examples¶
Here is a basic example of how to use the statistical functions:
#include <stdio.h>
#include <gsl/gsl_rstat.h>
int
main(void)
{
double data[5] = {17.2, 18.1, 16.5, 18.3, 12.6};
double mean, variance, largest, smallest, sd,
rms, sd_mean, median, skew, kurtosis;
gsl_rstat_workspace *rstat_p = gsl_rstat_alloc();
size_t i, n;
/* add data to rstat accumulator */
for (i = 0; i < 5; ++i)
gsl_rstat_add(data[i], rstat_p);
mean = gsl_rstat_mean(rstat_p);
variance = gsl_rstat_variance(rstat_p);
largest = gsl_rstat_max(rstat_p);
smallest = gsl_rstat_min(rstat_p);
median = gsl_rstat_median(rstat_p);
sd = gsl_rstat_sd(rstat_p);
sd_mean = gsl_rstat_sd_mean(rstat_p);
skew = gsl_rstat_skew(rstat_p);
rms = gsl_rstat_rms(rstat_p);
kurtosis = gsl_rstat_kurtosis(rstat_p);
n = gsl_rstat_n(rstat_p);
printf ("The dataset is %g, %g, %g, %g, %g\n",
data[0], data[1], data[2], data[3], data[4]);
printf ("The sample mean is %g\n", mean);
printf ("The estimated variance is %g\n", variance);
printf ("The largest value is %g\n", largest);
printf ("The smallest value is %g\n", smallest);
printf( "The median is %g\n", median);
printf( "The standard deviation is %g\n", sd);
printf( "The root mean square is %g\n", rms);
printf( "The standard devation of the mean is %g\n", sd_mean);
printf( "The skew is %g\n", skew);
printf( "The kurtosis %g\n", kurtosis);
printf( "There are %zu items in the accumulator\n", n);
gsl_rstat_reset(rstat_p);
n = gsl_rstat_n(rstat_p);
printf( "There are %zu items in the accumulator\n", n);
gsl_rstat_free(rstat_p);
return 0;
}
The program should produce the following output,
The dataset is 17.2, 18.1, 16.5, 18.3, 12.6
The sample mean is 16.54
The estimated variance is 5.373
The largest value is 18.3
The smallest value is 12.6
The median is 17.2
The standard deviation is 2.31797
The root mean square is 16.6694
The standard devation of the mean is 1.03663
The skew is -0.829058
The kurtosis -1.2217
There are 5 items in the accumulator
There are 0 items in the accumulator
This next program estimates the lower quartile, median and upper
quartile from 10,000 samples of a random Rayleigh distribution,
using the 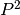 algorithm of Jain and Chlamtec. For
comparison, the exact values are also computed from the sorted
dataset.
algorithm of Jain and Chlamtec. For
comparison, the exact values are also computed from the sorted
dataset.
#include <stdio.h>
#include <stdlib.h>
#include <gsl/gsl_rstat.h>
#include <gsl/gsl_statistics.h>
#include <gsl/gsl_rng.h>
#include <gsl/gsl_randist.h>
#include <gsl/gsl_sort.h>
int
main(void)
{
const size_t N = 10000;
double *data = malloc(N * sizeof(double));
gsl_rstat_quantile_workspace *work_25 = gsl_rstat_quantile_alloc(0.25);
gsl_rstat_quantile_workspace *work_50 = gsl_rstat_quantile_alloc(0.5);
gsl_rstat_quantile_workspace *work_75 = gsl_rstat_quantile_alloc(0.75);
gsl_rng *r = gsl_rng_alloc(gsl_rng_default);
double exact_p25, exact_p50, exact_p75;
double val_p25, val_p50, val_p75;
size_t i;
/* add data to quantile accumulators; also store data for exact
* comparisons */
for (i = 0; i < N; ++i)
{
data[i] = gsl_ran_rayleigh(r, 1.0);
gsl_rstat_quantile_add(data[i], work_25);
gsl_rstat_quantile_add(data[i], work_50);
gsl_rstat_quantile_add(data[i], work_75);
}
/* exact values */
gsl_sort(data, 1, N);
exact_p25 = gsl_stats_quantile_from_sorted_data(data, 1, N, 0.25);
exact_p50 = gsl_stats_quantile_from_sorted_data(data, 1, N, 0.5);
exact_p75 = gsl_stats_quantile_from_sorted_data(data, 1, N, 0.75);
/* estimated values */
val_p25 = gsl_rstat_quantile_get(work_25);
val_p50 = gsl_rstat_quantile_get(work_50);
val_p75 = gsl_rstat_quantile_get(work_75);
printf ("The dataset is %g, %g, %g, %g, %g, ...\n",
data[0], data[1], data[2], data[3], data[4]);
printf ("0.25 quartile: exact = %.5f, estimated = %.5f, error = %.6e\n",
exact_p25, val_p25, (val_p25 - exact_p25) / exact_p25);
printf ("0.50 quartile: exact = %.5f, estimated = %.5f, error = %.6e\n",
exact_p50, val_p50, (val_p50 - exact_p50) / exact_p50);
printf ("0.75 quartile: exact = %.5f, estimated = %.5f, error = %.6e\n",
exact_p75, val_p75, (val_p75 - exact_p75) / exact_p75);
gsl_rstat_quantile_free(work_25);
gsl_rstat_quantile_free(work_50);
gsl_rstat_quantile_free(work_75);
gsl_rng_free(r);
free(data);
return 0;
}
The program should produce the following output,
The dataset is 0.00645272, 0.0074002, 0.0120706, 0.0207256, 0.0227282, ...
0.25 quartile: exact = 0.75766, estimated = 0.75580, error = -2.450209e-03
0.50 quartile: exact = 1.17508, estimated = 1.17438, error = -5.995912e-04
0.75 quartile: exact = 1.65347, estimated = 1.65696, error = 2.110571e-03
References and Further Reading¶
The algorithm used to dynamically estimate 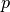 -quantiles is described
in the paper,
-quantiles is described
in the paper,
R. Jain and I. Chlamtac. The P^2 algorithm for dynamic calculation of quantiles and histograms without storing observations, Communications of the ACM, Volume 28 (October), Number 10, 1985, p. 1076-1085.